
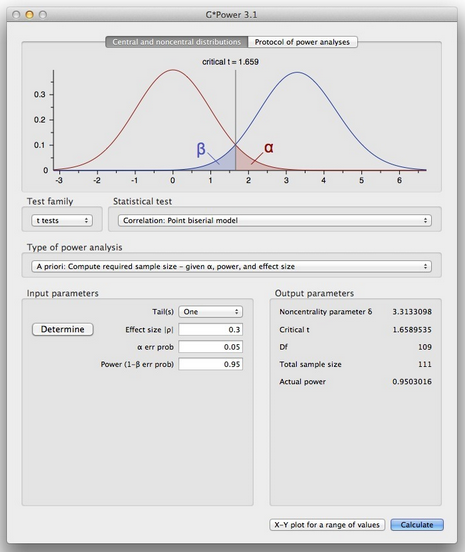
Analysts frequently base these estimates on pilot studies and historical research data. We need to enter an estimate for the standard deviation of material strength. Standard deviation is the field where we enter the data variability. We’ll enter a power of 0.9 so that the 2-sample t-test has a 90% chance of detecting a difference of 5. The proper value to enter in this field depends on norms in your study area or industry. If you hold the other input values constant and increase the test’s power, the required sample size also increases. This field is where you define the “reasonable chance” that I mentioned earlier. Power values is where we specify the probability that the statistical hypothesis test detects the difference in the sample if that difference exists in the population. This value helps prevent us from collecting an unnecessarily large sample.įor our example, we’ll enter 5 because smaller differences are unimportant for our process. It would not be worthwhile to expend resources to detect them.īy choosing this value carefully, you tailor the experiment so that it has a reasonable chance of detecting useful differences while allowing smaller, non-useful differences to remain potentially undetected. In other words, you consider smaller differences to be inconsequential. Instead, use your expertise to identify the smallest difference that is still meaningful for your application. Do not enter your guess for the difference between the two types of material. Differencesĭifferences is often a confusing value to enter.
#GPOWER EFFECT SIZE F SOFTWARE#
First off, we will leave Sample sizes blank because we want the software to calculate this value. We’ll go through these fields one-by-one. In a power and sample size analysis, statistical software presents you with a dialog box something like the following: Furthermore, we’ve tested these materials in a pilot study, which provides background knowledge for the estimates. If one type of material is significantly stronger than the other, we’ll use that material in our process.
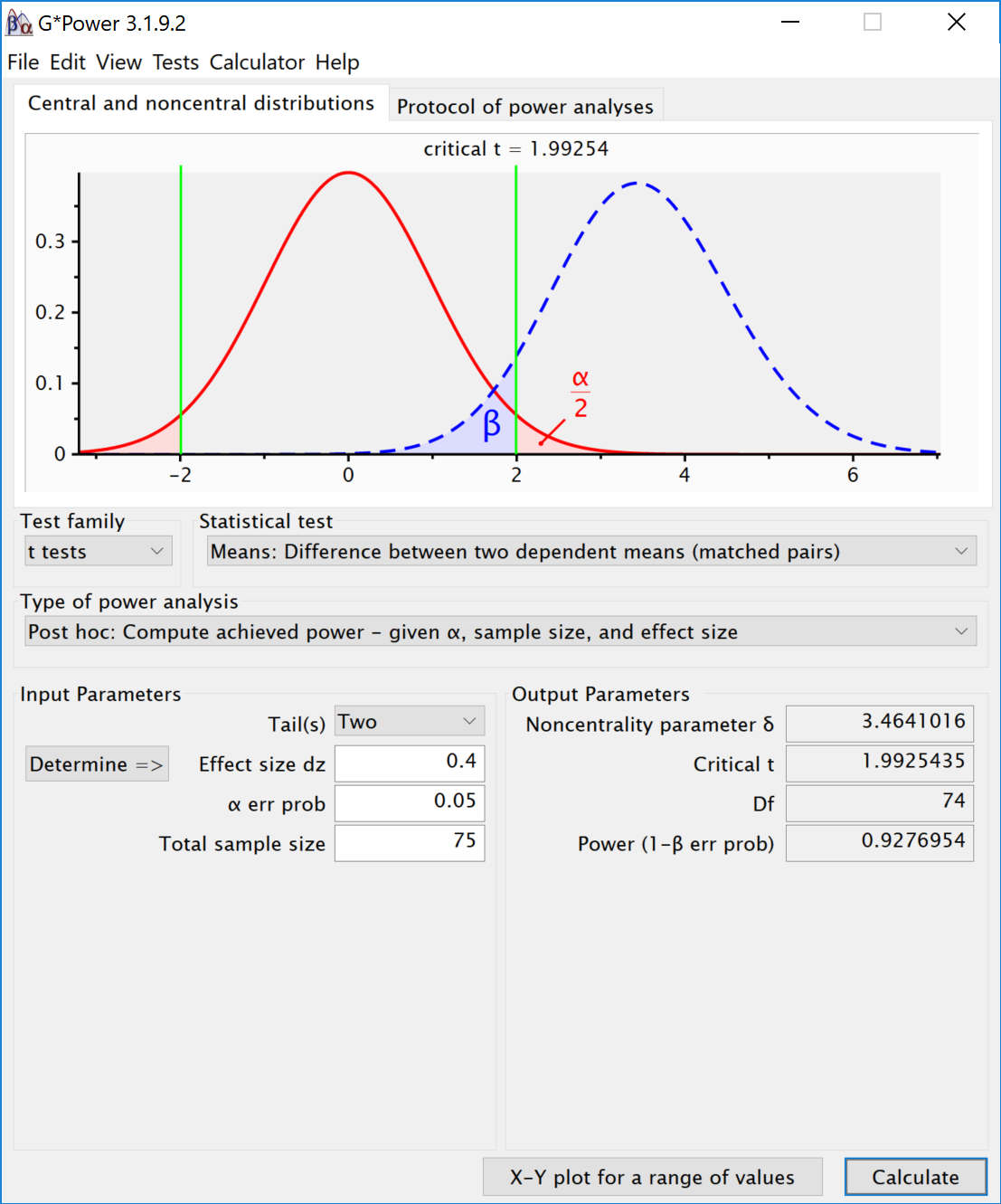
Suppose we’re conducting a 2-sample t-test to determine which of two materials is stronger. 2-Sample t-Test Power Analysis for Sample Size Let’s work through some examples in different scenarios to bring this to life.
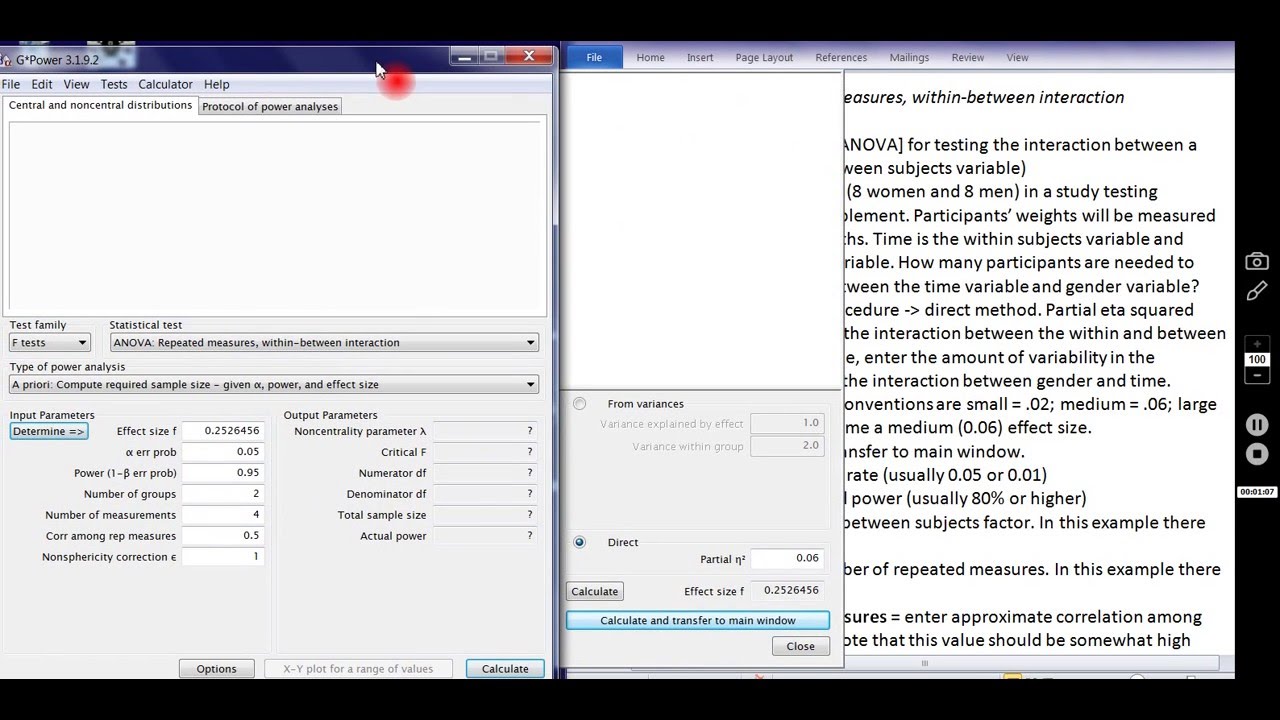
For instance, if you specify the smallest effect size that is practically significant, variability, and power, the software calculates the required sample size. Typically, you specify three of the four factors discussed above and your statistical software calculates the remaining value. In fact, going through this procedure forces you to focus on the relevant information. The power of the test depends on the other three factors.Īll of these details might sound complicated, but a statistical power analysis helps you manage them. Consequently, power is inversely related to a Type II error. In other words, the test correctly rejects a false null hypothesis. Statistical power is the probability that a hypothesis test correctly infers that a sample effect exists in the population. Related post: How Hypothesis Tests Work Statistical Power of a Hypothesis Testīecause we’re talking about determining the sample size for a study that has not been performed yet, you need to learn about a fourth consideration-statistical power. Consequently, you cannot determine a good sample size in a vacuum because the three factors are intertwined. The key takeaway is that the statistical significance of any effect depends collectively on the size of the effect, the sample size, and the variability present in the sample data. Hypothesis testing takes all of this information and uses it to calculate the p-value-which you use to determine statistical significance. If the sample data in Study A have sufficient variability, random error might be responsible for the large difference.


 0 kommentar(er)
0 kommentar(er)
